Les graphes

(Ce laboratoire en profite en passant pour vous faire apprendre plein de nouveaux trucs sur le C#. Conséquemment, les sections en bleu appelées "Pour votre culture C#" présentent des notions théoriques et des explications nécessaires pour arriver à faire le labo correctement. Considérez ces sections comme des notes de cours!)

Un graphe est un ensemble de noeuds (normalement appelés sommets) qui sont reliés par des arêtes. Chaque sommet peut être le point de départ ou d'arrivée de tout nombre d'arêtes (il n'y a pas de maximum).

Un sommet peut contenir n'importe quelle information - l'exemple ici montre des sommets qui ne contiennent que des nombres entiers.

Un graphe peut être orienté ou non. Un graphe orienté a des flèches sur ses arêtes indiquant qu'il est possible de passer d'un sommet A à un sommet B, mais pas de B à A. Il est toutefois possible dans un graphe orienté de voir deux arêtes relier deux sommets, chacune dans un sens.

Une arête peut également avoir un coût, c'est à dire un nombre associé à l'arête (et non à un des sommets). Ce coût peut représenter un coût monétaire, une distance ou n'importe quel autre concept selon le graphe. Lorsqu'une arête a un coût, il faut "payer" ce coût pour passer d'un sommet à l'autre.

Un graphe peut être utilisé pour représenter n'importe quelle situation de la vie courante dans laquelle on doit passer par plusieurs étapes pour atteindre un but. Les sommets peuvent représenter les pièces d'une maison (ou d'un donjon!), les coins de rues dans une ville, des ordinateurs sur un réseau, des personnes dans un entourage ou des décisions dans un algorithme.

Les graphes sont couramment utilisés en recherche opérationnelle. La recherche opérationnelle est la science qui s'occupe de trouver des solutions à des problèmes combinatoires (des problèmes comprenant un grand nombre de solutions possibles et pour laquelle on cherchera la solution optimale) ou d'autres genres de problèmes similaires.

Le problème du plus court chemin

Un problème classique lorsque l'on implémente des graphes est de trouver le plus court chemin entre deux sommets donnés. Le problème est beaucoup plus intéressant lorsque l'on utilise un graphe où les arêtes ont des coûts. Dans notre cas, on peut aisément supposer que les sommets représentent des noeuds du réseau (des routeurs et ordinateurs) et les coûts des arêtes représentent la vitesse de transmission des données d'un noeud à l'autre (plus le coût est grand, plus le temps requis pour les données est long).

Il existe beaucoup d'algorithmes pour trouver le plus court chemin dans un graphe. Le plus connu est probablement celui de Dijkstra (ça se prononce comme "Déïkstra"), algorithme nommé en l'honneur de son créateur, Edsger Wybe Dijkstra. C'est un algorithme qui garantit de trouver le plus court chemin possible en ne considérant jamais le même sommet deux fois.

Votre travail pour ce labo

Vous devrez produire tout d'abord une classe Sommet, un classe Arête et une classe Graphe qui permettent de représenter des graphes en mémoire. Ces graphes ne seront pas orientés (donc toute arête est traversable dans les deux directions) et chaque arête aura un coût entier associé. Les sommets ne contiendront qu'un simple numéro qui permettra de les identifier.

Vous devrez également intégrer une méthode Dijkstra à votre classe Graphe - cette méthode permettra soit de trouver le plus court chemin entre deux sommets, ou le plus court chemin entre un sommet de départ et tous les autres sommets du graphes (au choix de l'utilisateur). Si vous préférez explorer un autre algorithme de plus court chemin (car il en existe bien d'autres), vous pouvez également le faire.

Vous devrez respecter les spécifications suivantes pour éviter de perdre des points:

La classe Sommet

Le Sommet est la base du Graphe puisque le Graphe contiendra un tableau de Sommets. Tout ce qu'on a besoin d'y stocker pour qu'un sommet puisse exister, c'est un numéro d'identification, mais vous aurez besoin d'ajouter quelques attributs supplémentaires pour que votre méthode Dijkstra (et ça sera sans doute vrai pour toute autre méthode) puisse fonctionner plus facilement (voir plus bas).

Pour votre culture C# - les propriétés

On déclare une propriété en faisant simplement:

public int numero
{
    get
    {
        return numero_;
    }

    set
    {
        numero_ = value;
    }
}

La propriété est accessible de l'extérieur comme si on manipulait directement l'attribut qu'elle cache. On fera par exemple:

Sommet s = new Sommet();

s.numero = 12;
Console.WriteLine(s.numero);

Ici, on accède à numero en écriture, puis en lecture, comme si on manipulait un attribut. L'attribut (numero_) est en réalité privé. Évidemment, on peut ajouter beaucoup plus aux sections get et set de notre propriété afin de contrôler les entrées et les sorties. On peut même omettre une des deux sections (généralement le set).

Dans le cas du set, le paramètre implicite value n'a pas besoin d'être déclaré, mais il existe automatiquement dans la section set et contient la valeur qui a été passée à la propriété (dans notre exemple, 12).

Pour votre culture C# - L'override de ToString

La méthode ToString est reçue par héritage de la classe Object, parent implicite de toute classe en .NET. En C#, on ne peut avoir qu'un seul parent, sauf pour Object qui est toujours là implicitement. La méthode ToString est déclarée virtual dans Object et on est donc invités à l'overrider dans nos classes. Le but est simplement de retourner une chaîne de caractères qui identifie l'objet - on parle en fait de convertir l'objet en string. Du coup, toute fonction acceptant un string acceptera aussi un objet de notre classe, qui sera converti sur-le-champ. Par exemple:

public override string ToString()
{
    return "Bla bla";
}

La classe Arête

On ne stockera pas d'Arêtes directement dans le graphe (vous verrez comment elles seront représentées), mais les Arêtes pourront être utilisées comme "enrobage" pour passer de l'information entre le graphe et l'utilisateur. On pourra recevoir ou passer une arête pour représenter conceptuellement le lien qui existe entre deux Sommets. Une Arête doit contenir:

La classe Graphe

Il existe bien des façons d'implémenter un graphe en mémoire. Nous opterons ici pour une des solutions populaires et efficaces: un tableau de sommets et une matrice de coûts à deux dimensions (représentant en fin de compte les arêtes) qui indiquera le coût à payer pour passer d'un sommet à un autre. C'est évidemment cette classe qui est la plus complexe du lot.

Le graphe contiendra donc:

Pour votre culture C# - Les tableaux

Un tableau en C# est un objet à part entière, une instance de la classe System.Array. Toutefois il n'est pas permis d'instancier un Array directement (en réalité Array est une classe abstraite), on doit utiliser les éléments du langage prévu à cet effet. Par exemple:

int[] tableau; // Déclaration d'un tableau d'entiers.   // À ce point-ci tableau pointe vers null.      
tableau = new int[5]; // Instanciation du tableau.  

// À ce point-ci, tableau pointe vers un tableau de 5 entiers non-initialisés, donc contenant des 0.  

Les avantages de traiter un tableau comme un objet contenant une collection de données plutôt que comme un ensemble de données placées de façon contiguë en mémoire sont évidents. Premièrement, pas besoin de se casser la tête avec la gestion de la mémoire (et pas de risque de lire des données erronnées si on sort des bornes du tableau). Deuxièmement, notre objet tableau contient tout un tas de méthodes et de propriétés héritées de System.Array qui peuvent nous être fort utiles dans la gestion et la manipulation de nos données (allez les découvrir, vous verrez).

On peut initialiser les données du tableau à l'instanciation en faisant simplement:

tableau = new int[5] {1,3,45,-10,133};

(et si on fait comme ça, on peut omettre l'indice dimensionnel du tableau qui sera ajusté au nombre de données.)

On accède à une case du tableau par son index, en faisant tableau[0] = 12 par exemple. Notez que l'indice dimensionnel donné à l'instanciation du tableau représente le nombre d'éléments et que ces éléments sont numérotés à partir de 0 (donc un int[5] contient 5 int, de 0 à 4).

Dans le cas d'un tableau d'objets (et non de types valeurs), on fera par exemple:

Sommet[] tableau;  
tableau = new Sommet[10];

Notez qu'à ce point-ci, tableau pointe vers un tableau de dix Sommets, mais chacun de ces Sommets (tableau[0], tableau[1], ..., tableau[9]) pointe vers null puisqu'ils n'ont pas encore été instanciés. Chacun des Sommets du tableau devra en effet être instancié pour être utilisé.

Pour votre culture C# - Les propriétés statiques

Une propriété statique sera accessible au niveau de la classe plutôt qu'au niveau d'un objet précis. Par exemple, on fera Sommet.infini plutôt que s.inifini pour obtenir cette valeur. On utilise les membres statiques lorsque leur fonction ne relève pas d'un objet précis (comme dans ce cas-ci, où l'infini est toujours le même). Du coup, on remarque qu'une propriété peut retourner n'importe quoi, qui n'a pas besoin d'être un attribut au départ...

On ajoutera simplement le mot-clé static après public.

Pour votre culture C# - Les itérateurs

Un itérateur est une fonctionnalité fort intéressante qui nous permet de prendre en charge l'instruction foreach dans une classe. En effet, il est possible de faire, avec un tableau par exemple, quelque chose comme:

int[] tab = new int[10];   
foreach (int i in tab)   
{
    Console.WriteLine(i);
}

L'instruction foreach parcourt simplement le tableau d'un bout à l'autre, sans qu'on ait besoin de lui donner les dimension du tableau - tout cela est implicite au tableau lui-même.

Concrètement, l'instruction foreach cache la complexité de l'interface IEnumerator de l'espace de noms System.Collections. Il est en effet possible d'utiliser la méthode GetEnumerator() d'un tableau pour obtenir un IEnumerator contenant les membres MoveNext, Reset et Current qu'on peut utiliser pour parcourir le tableau. Par exemple, ceci est valide:

IEnumerator ie = tab.GetEnumerator();  
for (int i = 0; i < tab.GetLength(0); i++)  
{   
    ie.MoveNext();  
    Console.WriteLine(ie.Current);  
}

En fait, lorsqu'on utilise le foreach, c'est exactement ce qui se passe mais de façon cachée.

Sachant cela, il est possible de créer des classes implémentant l'interface IEnumerator à leur façon, définissant MoveNext, Reset et Current comme on le désire. Toutefois c'est un peu compliqué inutilement.

C'est là qu'interviennent les itérateurs. Ils nous permettent de prendre en charge le foreach sans devoir implémenter au complet IEnumerator. Concrètement:

La façon la plus simple de créer un itérateur est d'implémenter la méthode GetEnumerator(). Elle peut fonctionner comme on veut, tant qu'elle utilise yield return successivement pour retourner plusieurs éléments du même type. Par exemple, ceci:

using System.Collections;    

public class test 
{
     public IEnumerator GetEnumerator()
     {
        yield return "les";
        yield return "itérateurs";
        yield return "c'est";
        yield return "cool";
     }
}

class Program   
{
      static void Main(string[] args)
      {
          foreach (string i in new test())

              Console.Write(i + " ");
      }
}

Produira la sortie:

Les itérateurs c'est cool

Notre itérateur peut faire partie de n'importe quelle classe et retourner n'importe quoi (tant qu'il s'agira de données du même type) de n'importe quelle façon. Tant qu'il s'appelle GetEnumerator(), a un type de retour IEnumerator et utilise yield return, toutes les méthodes de IEnumerable seront implémentées automatiquement pour nous et notre classe supportera le foreach.

Pour votre culture C# - Les itérateurs nommés

On peut également définir plusieurs itérateurs différents dans une classe et à ce moment-là en utiliser un en particulier dans notre foreach. Lorsqu'on ne précise aucun itérateur au foreach, il utilise GetEnumerator().

Un itérateur nommé doit être de type IEnumerable. Il peut avoir n'importe quel nom et même accepter des paramètres. Il doit utiliser yield return pour retourner plusieurs valeurs du même type.

Pour l'utiliser avec le foreach, on devra explicitement passer un itérateur à "in" plutôt qu'une simple instance d'un objet. Par exemple:

using System.Collections;          

public class test 
{
     public IEnumerator GetEnumerator()
     {
        yield return "les";
        yield return "itérateurs";
        yield return "c'est";
        yield return "cool";
     }

     public IEnumerable itérateurNumérique(int début, int fin)
     {
        for (int i = début; i <= fin; i++)
           yield return i;
     }
} 

class Program
{
      static void Main(string[] args)
      {
          foreach (int i in new test().itérateurNumérique(10,20))

              Console.Write(i + " ");

       }
}

Produira la sortie:

10 11 12 13 14 15 16 17 18 19 20

Remarquez que nos deux itérateurs habitent côte à côte dans la classe test sans aucun problème.

• Notons qu'on ne voudra pas modifier le nombre de sommets d'un graphe - on définira ce nombre à la construction et on n'enlèvera ni n'ajoutera jamais de sommets. Ceci nous permettra de garder nos classes simples et d'éviter de la manipulation de tableaux souvent fort coûteuse (si jamais on prévoyait que le nombre de sommets d'un graphe risquait de changer couramment lors d'une exécution, il serait plus sage d'implémenter notre graphe comme une liste de sommets, chacun contenant une liste de pointeurs vers ses voisins).

   

• Une méthode void Dijkstra(Sommet départ, Sommet cible) qui calculera les plus courts chemins:
• Si départ est null, Dijkstra utilisera le Départ du Graphe (c'est un attribut). Si le Départ du Graphe est aussi null, Dijkstra affichera un message d'erreur et ne fera rien.
• Si cible est null, Dijkstra calculera le plus court chemin pour tous les sommets du graphe, partant du sommet de départ.
• Si cible est définie, Dijkstra calculera le plus court chemin entre départ et cible.

Tout ceci nous permettra de définir aisément un graphe comme ceci:

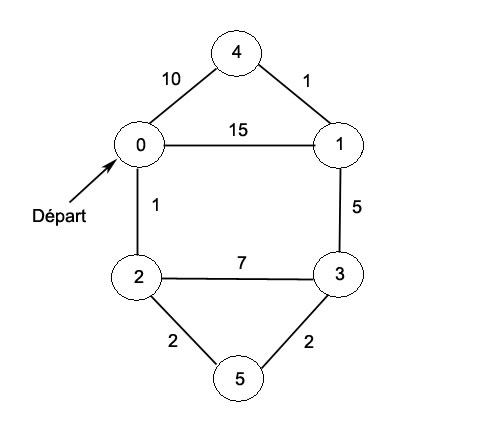
en faisant quelque chose comme:

Graphe g = new Graphe(6);

g.AjouterArête(0, 1, 15);
g.AjouterArête(0, 2, 1);
g.AjouterArête(2, 3, 7);
g.AjouterArête(3, 1, 5);
g.AjouterArête(0, 4, 10);
g.AjouterArête(4, 1, 1);
g.AjouterArête(2, 5, 2);
g.AjouterArête(5, 3, 2);

g.Départ = g.Sommets[0];

Évidemment, les sommets sont numérotés à partir de 0.

Pour votre culture C# - Les indexeurs

Vous aurez peut-être remarqué que mon exemple ci-haut appelle g.Sommets[0] comme si de rien n'était. On se rappelle que sommets_ est un attribut privé et on supposé que Sommets est une propriété publique qui expose sommets_. Mais comme sommets_ est un tableau Sommets[], la propriété devra donc être du même type et permettre de retourner le tableau au complet. Comment faire pour retourner juste une case?

On peut utiliser les indexeurs, qui ne sont rien d'autres que des propriétés indexées prévues justement pour faire ça. On les déclare ainsi:

public Sommet this[int i]
{
    get { return sommets_[i]; }
    set { sommets_[i] = value; }
}

Simple, n'est-ce pas? Le mot-clé this représente l'objet lui-même, donc le Sommet. On déclare une propriété public Sommet qui s'appelle nom_de_l_objet[i]... Et le i est un int. À l'intérieur, on retourne ou modifie une case du tableau (attribut) correspondant en utilisant l'index i.

Ce bout de code peut donc être copié tel quel dans votre programme! Cadeau!

L'algorithme de Dijkstra

L'algorithme de Dijkstra n'est pas compliqué. Chaque sommet doit pouvoir contenir un nombre représentant sa distance totale du sommet de départ et un pointeur vers le sommet précédent dans l'itinéraire trouvé jusqu'à présent. On modifiera ces valeurs tout au long de notre recherche. En effet, on trouvera le chemin le plus court en partant du point de départ et en explorant dans toutes les directions, privilégiant à chaque étape le chemin le moins coûteux jusqu'à présent. Lorsqu'on atteindra la cible voulue, on n'aura qu'à revenir en arrière en suivant les pointeurs vers le sommet précédent jusqu'au point de départ.

Au départ, tous les noeuds sont à une distance infinie du sommet de départ (donc non déterminée), sauf le sommet de départ qui est à une distance de 0 (bien sûr). Lorsque l'on parlera de la "distance" d'un sommet, cela signifiera "sa distance du sommet de départ tel que calculée jusqu'à maintenant".

L'algorithme sélectionnera le sommet ayant la plus petite distance parmi tous les sommets qu'il n'a pas encore visités (la première fois, ce sera nécessairement le sommet de départ, le seul qui n'a pas une distance infinie). Ce sommet sera appelé le sommet courant.

On trouvera ensuite tous les voisins du sommet courant. Pour chaque voisin, si la distance du sommet courant + le coût de l'arête entre le sommet courant et le sommet voisin est plus petite que la distance du voisin, cela signifie qu'on a trouvé un chemin moins coûteux pour atteindre ce sommet voisin. Dans ce cas on modifiera la distance du voisin pour la mettre égale à celle du sommet courant + le coût de l'arête jusqu'au voisin, puis on fera pointer le pointeur "précédent" du voisin vers le sommet courant, nous permettant ainsi de revenir en arrière jusqu'au point de départ.

Une fois qu'on a ainsi traité tous les voisins du sommet courant, on marque le sommet courant comme ayant déjà été visité, puis on recommence l'algorithme, sélectionnant le sommet qui a la distance la plus petite parmi tout ceux qui n'ont pas encore été visités.

Si on veut atteindre une cible en particulier, on peut arrêter lorsque le sommet courant est égal à cette cible. En effet, une fois qu'on en est là, tout calcul supplémentaire ne ferait que nous éloigner de la cible et tout autre sommet qui n'a jamais été visité encore a une distance plus grande que la cible (et donc ne pourra jamais nous faire atteindre la cible par un chemin plus court). Si on veut calculer les distances pour tous les sommets du graphe, on continuera jusqu'à ce qu'il n'y ait plus de sommets qui n'ont jamais été visités.

Retrouver notre chemin

Une fois que Dijkstra a terminé sa magie, on peut partir de la cible (ou de n'importe quel sommet si on a calculé tout le graphe) et suivre les pointeurs "précédents" pour trouver le chemin de la cible au point de départ. Une bonne façon de les inverser afin d'avoir un chemin à l'endroit est de les pousser sur une pile puis de les "dépiler".

On peut faire par exemple:

g.Dijkstra(null,g.Sommets[1]);  // Ceci trouve le plus court chemin entre le point
  // de départ du graphe jusqu'au sommet 1 du graphe.
  
Stack<Sommet> pile = new Stack<Sommet>();  // On instancie une pile de Sommets
Sommet unSommet = g.Sommets[1]; // On part de la fin
Console.WriteLine("Meilleur chemin de {0} à {1}: longueur {2}", g.Départ, g.Sommets[1], unSommet.Distance);

while (unSommet != null)
{
   pile.Push(unSommet);  // On empile chaque sommet
   unSommet = unSommet.Précédent; // puis on recule
} // jusqu'à ce qu'il n'y ait plus de précédent (donc au point de départ)

// Un foreach d'une pile énumère la pile de haut en bas sans en modifier le contenu
foreach (Sommet ss in pile)
   Console.WriteLine("{0} (distance {1})", ss.Numéro, ss.Distance);

La remise

Comme ce laboratoire est d'envergure, vous aurez deux semaines pour y travailler. Vous devrez donc remettre par courriel à votre charmant professeur un fichier .cs contenant vos classes Arête, Sommet et Graphe, sans Main. Ne faites pas de copier/coller de texte. Votre courriel doit me parvenir au plus tard vendredi le 30 septembre à 8h55. La période de laboratoire du 23 septembre sera également consacrée à ce travail.

Je vous conseille de commencer par faire les Arêtes, Sommets et Graphes sans vous soucier de Dijkstra. Lorsque vous pourrez représenter un graphe correctement en mémoire, attaquez-vous à la méthode Dijkstra (qui vous demandera de faire quelques ajouts à vos classes).

Et maintenant: graphologues amateurs, à vos claviers!