PROFDINFO.COM
Votre enseignant d'informatique en ligne
Bits et octets
Ordinateurs et système binaire
À l'intérieur d'un ordinateur, toute l'information (données, adresses, instructions) est manipulée et conservée à l'aide de millions de transistors qui agissent comme autant d'interrupteurs minuscules.
Étant donné qu'un interrupteur a seulement deux états possibles (fermé ou ouvert), toute l'information dans l'ordinateur peut être représentée à l'aide de nombres formés uniquement de 1 et de 0 qui correspondent respectivement à l'état fermé ou ouvert d'un transistor.
Un tel système de numérotation en base 2 s'appelle système binaire et ses chiffres, qui peuvent prendre comme valeur 1 ou 0, se nomment bits pour binary digits qui en anglais veut dire "chiffre binaire".
Principaux systèmes de numération utilisés
En plus du système binaire, le système hexadécimal (base 16) est beaucoup utilisé en informatique, notamment parce qu'il permet de "condenser" la représentation binaire (nous verrons plus tard comment).
Pour un programmeur, il est essentiel d'être à l'aise avec ces deux systèmes de numération et de pouvoir passer facilement de l'un à l'autre, non seulement pour déboguer plus facilement, mais aussi pour écrire des programmes plus robustes et plus efficaces.
Le tableau suivant présente les valeurs équivalentes en bases 2, 8, 10 et 16. TOUT BON INFORMATICIEN CONNAIT CE TABLEAU PAR COEUR !
BINAIRE (base 2) |
OCTAL (base 8) |
DÉCIMAL (base 10) |
HEXADÉCIMAL (base 16) |
0000 |
00 |
00 |
0 |
0001 |
01 |
01 |
1 |
0010 |
02 |
02 |
2 |
0011 |
03 |
03 |
3 |
0100 |
04 |
04 |
4 |
0101 |
05 |
05 |
5 |
0110 |
06 |
06 |
6 |
0111 |
07 |
07 |
7 |
1000 |
10 |
08 |
8 |
1001 |
11 |
09 |
9 |
1010 |
12 |
10 |
A |
1011 |
13 |
11 |
B |
1100 |
14 |
12 |
C |
1101 |
15 |
13 |
D |
1110 |
16 |
14 |
E |
1111 |
17 |
15 |
F |
Conversion entre systèmes de numération
Il existe plusieurs méthodes pour convertir des nombres d'un système de numération à l'autre. Quelques-unes vous sont présentées ici. Vous pouvez utiliser d'autres méthodes que celles-ci, mais à chaque fois que l'on vous demandera d'effectuer une conversion, prenez soin de bien indiquer votre démarche !
De décimal à binaire
On utilise la méthode dite "par divisions successives". Il s'agit de diviser par 2 le nombre à convertir, de diviser ensuite par 2 le résultat obtenu (quotient) et ainsi de suite, tant que ce résultat n'est pas égal à 0. On constitue la valeur binaire en assemblant les restes des divisions en commençant par la fin.
Exemple avec 75 :
75 / 2 = 37 reste 1
37 / 2 = 18 reste 1
18 / 2 = 9 reste 0
9 / 2 = 4 reste 1
4 / 2 = 2 reste 0
2 / 2 = 1 reste 0
1 / 2 = 0 reste 1 (le quotient égal à 0 indique la fin)
75 en base 10 s'écrit donc 1001011 en base 2.
Exemple avec 186 :
186 / 2 = 93 reste 0 93 / 2 = 46 reste 1 46 / 2 = 23 reste 0 23 / 2 = 11 reste 1 11 / 2 = 5 reste 1 5 / 2 = 2 reste 1 2 / 2 = 1 reste 0 1 / 2 = 0 reste 1
186 en base 10 s'écrit 10111010 en base 2.
Exemple avec 223 :
223 / 2 = 111 reste 1
111 / 2 = 55 reste 1
55 / 2 = 27 reste 1
27 / 2 = 13 reste 1
13 / 2 = 6 reste 1
6 / 2 = 3 reste 0
3 / 2 = 1 reste 1
1 / 2 = 0 reste 1
223 en base 10 s'écrit 11011111 en base 2.
De décimal à hexadécimal
Comme pour la conversion de décimal à binaire, on utilise la méthode par divisions successives, sauf que le diviseur est maintenant 16.
Exemple avec 75 :
75 / 16 = 4 reste 11 (B en hexadécimal) 4 / 16 = 0 reste 4 (le quotient égal à 0 indique la fin)
75 en base 10 s'écrit 4B en base 16.
Exemple avec 223 :
223 / 16 = 13 reste 15 (F en hexadécimal)
13 / 16 = 0 reste 13 (D en hexadécimal)
223 en base 10 s'écrit DF en base 16.
Exemple avec 1000 :
1000 / 16 = 62 reste 8
62 / 16 = 3 reste 14
3 / 16 = 0 reste 3
1000 en base 10 s'écrit 3E8 en base 16.
De binaire à décimal
On fait la somme des produits de chaque chiffre du nombre binaire par 2 élevé à la puissance n, où n est la position de ce chiffre dans le nombre. La position débute à 0 et va croissante à mesure que l'on se déplace vers la gauche.
Exemple avec 00110001 :
| Position | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Chiffre | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
(0 * 27) + (0 * 26) + (1 * 25) + (1 * 24) + (0 * 23) + (0 * 22) + (0 * 21) + (1 * 20)
(0 * 128) + (0 * 64) + (1 * 32) + (1 * 16) + (0 * 8) + (0 * 4) + (0 * 2) + (1 * 1)
(1 * 32) + (1 * 16) + (1 * 1)
32 + 16 + 1
49
00110001 en base 2 s'écrit 49 en base 10.
Exemple avec 11110000 :
(1 * 27) + (1 * 26) + (1 * 25) + (1 * 24)
128 + 64 + 32 + 16
240
11110000 en base 2 s'écrit 240 en base 10.
Exemple avec 001010101010 :
(1 * 29) + (1 * 27) + (1 * 25) + (1 * 23) + (1 * 21)
512 + 128 + 32 + 8 + 2
682
De binaire à hexadécimal
On fait des groupes de 4 bits en commençant à droite, on convertit en base 16 ces nombres (voir le tableau plus haut) et on les assemble.
Exemple avec 00110001 :
00110001 -> 0011 0001
3 1 (d'après le tableau)
00110001 en base 2 s'écrit 31 en base 16.
Exemple avec 11000101 :
11000101 -> 1100 0101
C 5
11000101 en base 2 s'écrit C5 en base 16.
Exemple avec 1010101010 :
101010101010 -> 0010 1010 1010
2 A A
1010101010 en base 2 s'écrit 2AA en base 16.
D'hexadécimal à binaire
On convertit chaque chiffre de la notation hexadécimale en un nombre binaire de 4 bits et on assemble.
Exemple avec 3F :
3F -> 3 F
0011 1111 (d'après le tableau)
3F en base 16 s'écrit 00111111 en base 2.
Exemple avec ABC :
ABC -> A B C
1010 1011 1100
ABC en base 16 s'écrit 101010111100 en base 2.
Exemple avec F502 :
F502 -> F 5 0 2
1111 0101 0000 0010
F502 en base 16 s'écrit 1111010100000010 en base 2.
D'hexadécimal à décimal
Comme pour la conversion de binaire à décimal, sauf que l'on utilise des puissances de 16.
Exemple avec A8 :
| Position | 1 | 0 |
| Chiffre | A | 8 |
(A * 161) + (8 * 160)
(10 * 16) + (8 * 1)
160 + 8
168
A8 en base 16 s'écrit 168 en base 10.
Exemple avec 340 :
(3 * 162) + (4 * 161) + (0 * 160)
(3 * 256) + (4 * 16)
768 + 64
832
340 en base 16 s'écrit 832 en base 10.
Exemple avec 10EE :
(1 * 4096) + (0 * 256) + (14 * 16) + (14 * 1)
4096 + 0 + 224 + 14
4334
10EE en base 16 s'écrit 4334 en base 10.
Unités de mesure de la mémoire
Les ordinateurs ne manipulent pas les bits individuellement, mais par groupes de 8, 16, 32 ou 64 bits. L'octet, qui représente un groupe de 8 bits, est l'unité de mesure de la mémoire utilsé dans le monde de l'informatique.
Les multiples de l'octet les plus utilisés sont :
- le kilo-octet (Ko) ou 210 octets, soit 1 024 octets;
- le méga-octet (Mo) ou 220 octets, soit 1 048 576 octets;
- le giga-octet (Go) ou 230 octets, soit 1 073 741 824 octets;
- le téra-octet (To) ou 240 octets, soit 1 099 511 627 776 octets;
- le péta-octet (Po) ou 250 octets, soit 1 125 899 906 842 624 octets.
Représentation des nombres en mémoire
Chaque langage de programmation offre des types de base dans lesquels les variables peuvent être déclarées. Le tableau suivant présente les types de base disponibles en C++ :
| Type | Signification | Taille (octets) | Plage de valeurs |
| char | caractère | 1 | -128 à 127 |
| unsigned char | caractère non signé | 1 | 0 à 255 |
| short int | entier court | 2 | -32 768 à 32 767 |
| unsigned short int | entier court non signé | 2 | 0 à 65 535 |
| int | entier | 4 (*) | -2 147 483 648 à 2 147 483 647 |
| unsigned int | entier non signé | 4 (*) | 0 à 4 294 967 295 |
| long int | entier long | 4 | -2 147 483 648 à 2 147 483 647 |
| unsigned long int | entier long non signé | 4 | 0 à 4 294 967 295 |
| long long int | entier très long | 8 | -9 223 372 036 854 775 808 à 9 223 372 036 854 775 807 |
| unsigned long long int | entier très long non signé | 8 | 0 à 18 446 744 073 709 551 615 |
| float | flottant | 4 | -3.4*10-38 à 3.4*1038 |
| double | flottant (double) | 8 | -1.7*10-308 à 1.7*10308 |
| bool | booléen | 1 | true ou false |
(*) la taille du int sera de 2 octets sur un processeur 16 bits, mais on n'en voit vraiment plus beaucoup de ceux-là!
Débordement et représentation des entiers négatifs
Que se passe-t-il si j'exécute ce petit programme?
#include <iostream>
using namespace std;
int main()
{
unsigned short s;
s = 65533;
cout << s << endl;
s = s + 1;
cout << s << endl;
s = s + 1;
cout << s << endl;
s = s + 1;
cout << s << endl;
s = s + 1;
cout << s << endl;
s = s + 1;
cout << s << endl;
}
Pas très complexe comme code... On commence avec 65 533, puis on ajoute 1 cinq fois en affichant le résultat chaque fois. Évidemment on pourrait s'attendre à quelque chose comme:
65533 65534 65535 65536 65537 65538
Mais en fin de compte, on se retrouve plutôt avec:
65533 65534 65535 0 1 2
Que se passe-t-il? C'est simple : le plus grand nombre qu'on peut mettre dans une variable de type unsigned short est 65 535 (c'est d'ailleurs indiqué dans le tableau ci-haut). Que se passe-t-il ici? On appelle cette situation un débordement (overflow en anglais) et c'est un peu similaire à avoir fait le "tour du compteur" avec un odomètre d'automobile : une fois passé le plus grand nombre possible, on revient au plus petit nombre possible et on continue d'augmenter à partir de là.
Notez que si vous changez la déclaration de la variable s pour qu'elle soit de type short, et que vous y mettez 32 765 comme point de départ, vous obtiendrez un résultat encore plus étrange : on retombe soudainement dans les négatifs.
32765 32766 32767 -32768 -32767 -32766
D'où proviennent ces nombres négatifs? Les variables de type signé utilisent le même nombre de bits que leur version unsigned (non signée). Elles peuvent donc représenter la même quantité de nombres (65 536 nombres différents dans le cas d'un short). Par contre, au lieu de ne représenter que des nombres positifs, on utilise la moitié de ces arrangements binaires pour représenter des nombres négatifs.
Lorsqu'une variable est de type signé, cela signifie que son dernier bit (celui à gauche) est un bit de signe. Lorsque ce bit est à 0, ça signifie que le nombre est positif et qu'on peut le convertir en décimal normalement pour connaître sa valeur. Si ce bit est à 1, ça signifie que le nombre est négatif. Malheureusement, dans ce cas, on ne peut pas simplement convertir les bits suivants pour connaître la valeur. Sachez que, pour éviter d'avoir deux représentations différentes pour le nombre 0 (0000 0000 qui représenterait +0 et 1000 0000 qui représenterait -0), on a plutôt opté pour la méthode du complément à deux pour représenter les nombres binaires négatifs. La méthode en elle-même ne sera pas couverte dans ce cours, mais retenez simplement que si le bit de signe (à gauche) est à 1 dans une variable de type signé, ça signifie qu'il est négatif et qu'on ne peut pas convertir le nombre en décimal comme on le ferait normalement.
Une représentation binaire, deux valeurs possibles
Cela signifie donc qu'un même nombre binaire en mémoire peut finalement représenter deux nombres différents. En effet, le nombre 1110 0111, par exemple, représente 231 s'il est placé dans une variable de type unsigned char, mais un nombre négatif s'il se trouve dans une variable de type char. Le type de données est donc crucial afin de connaître la valeur représentée par la chaîne binaire. En effet, tout ce qui se trouve dans la mémoire de l'ordinateur n'est qu'une série de 0 et de 1, mais la façon de les interpréter peut varier selon l'usage qu'on en fait.
On a vu comment représenter tous les nombres entiers, mais comment l'ordinateur fait-il pour conserver du texte en mémoire à l'aide de 0 et de 1 uniquement? La réponse est simple : il convertit les lettres en nombres, puis les stocke comme tous les autres nombres. Pour ce faire, il utilise un simple tableau où chaque caractère se voit assigner un nombre entre 0 et 255 (incluant plusieurs caractères non imprimables). Et dans quoi peut-on justement stocker un nombre de 0 à 255? Dans un char! Ça explique d'ailleurs pourquoi ce type de données s'appelle char... pour character! À la base, il est fait pour stocker un caractère, mais comme un caractère est au final un nombre de 0 à 255, on peut aussi y stocker des nombres directement.
Cette norme s'appelle ASCII, qui signifie American Standard Code for Information Interchange (ou code standard américain pour l'échange d'information). Elle existe depuis 1963 et est encore utilisée aujourd'hui. Vous pouvez consulter les tables ASCII ici.
Utiliser une variable de type char pour contenir des petits nombres afin de gaspiller le moins de mémoire possible peut être une bonne idée. Toutefois, lorsque l'on veut faire des cin et des cout avec ces variables, la solution est à éviter.
En effet, essayez ceci:
#include <iostream>
using namespace std;
int main()
{
char c;
char cplus10;
cout << "Entrez votre age : ";
cin >> c;
cplus10 = c + 10;
cout << "Dans 10 ans vous aurez " << cplus10 << " ans!" << endl;
}
Quel étrange résultat :
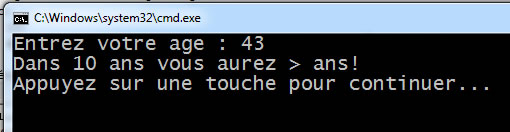
C'est le problème avec les char : ils sont conçus pour contenir un caractère, à la base. Lorsqu'on les affiche à l'écran, ce n'est pas le nombre qu'ils contiennent qui est affiché, mais le caractère correspondant à ce nombre dans la table ASCII! Pas très pratique...
On pourrait alors modifier le code pour ne pas afficher directement un char:
#include <iostream>
using namespace std;
int main()
{
char c;
cout << "Entrez votre age : ";
cin >> c;
cout << "Dans 10 ans vous aurez " << c + 10 << " ans!" << endl;
}
c + 10, même si c est un char, retourne un int, puisque 10 est considéré comme un int. Et afficher un int nous montrera le nombre et non pas le caractère qui y correspond. Toutefois, résultat toujours étrange :
On vieillit vite avec cette méthode! Qu'est-ce qui s'est passé? Est-ce impossible d'additionner un nombre à un char? Pourtant non, le problème est ailleurs. L'explication est simple : si un cout de char affiche le caractère qui correspond au nombre qu'il contient, un cin dans un char lira un seul caractère et stockera le nombre qui y correspond selon la norme ASCII dans la variable.
Dans l'exemple ci-haut, lorsque je tape 43, le cin placera uniquement le caractère 4 dans la variable c, puisque c'est un char. Et le code ASCII du caractère 4 est... 52! Le calcul c + 10 est donc valide, c n'a simplement jamais contenu 43.
Où s'en va le 3 du 43 alors? Il reste en attente et s'en ira dans le prochain cin qui sera fait. Essayez de faire un cin juste après cin >> c et vous verrez ce qui se passe.
La leçon à tirer de tout ça : si vous tenez à utiliser des char pour stocker des nombres, ne les utilisez pas directement dans un cin ou un cout. Utilisez une variable de type short ou int, que vous pourrez ensuite affecter à votre char.
Et les autres langues?
Aujourd'hui, on se déplace lentement vers la norme Unicode, qui assigne aussi un nombre à chaque caractère, mais qui encode ces nombres sur 1 à 4 octets (selon ce qui est nécessaire, dans le but d'économiser de l'espace tant que possible), ce qui permet donc de représenter les caractères de la plupart des alphabets du monde. On doit alors utiliser l'encodage UTF-8, UTF-16 ou UTF-32 pour représenter tout ça. Notez que les 128 premiers caractères ASCII ont le même code en Unicode et s'encodent sur un seul octet, par souci de compatibilité. Le C++ natif ne supporte pas Unicode par défaut et fonctionne en ASCII.
Exercices
Question 1
Remplissez le tableau suivant en faisant les conversions nécessaires. Fournissez des traces de votre démarche:
Binaire |
Décimal |
Hexadécimal |
11001010 |
||
181 |
||
D7 |
||
357 |
||
11101011 |
||
37 |
||
FED |
||
01010101 |
||
143 |
Question 2
Indiquez si les nombres binaires suivants sont positifs ou négatifs. S'ils sont positifs, donnez leur valeur en décimal. Faites attention au type de données!
a) 1011 0101 (unsigned char)
b) 1011 0101 (char)
c) 1111 1111 0010 0011 (short int)
d) 1111 1111 0010 0011 (unsigned short int)
e) 0111 0101 (unsigned char)
f) 0111 0101 (char)
Question 3
Que signifie cette chaîne binaire, si on sait qu'elle est constituée de 6 chars dans le but de représenter un mot?
0100 1100 // 0110 1001 // 0110 1111 // 0110 1110 // 0110 0101 // 0110 1100